Visualisation, Spatial Reasoning and AI for Problem Solving in Mathematics.

Part 1

It is important to explicitly value the visualising and thinking children engage in and not just focus on the correct final answers.

Far too often children jump into performing a calculation without appreciating the full task or problem and the ‘components’ actually needed.

Gestures and talk are likely to be early demonstrations of children’s visualisation, and this is best achieved by delaying access to recording materials, giving children the opportunity to interact before ‘diving into’ a pool of mathematics.

Children need to have enough time to secure an understanding of the problem and a strategy before they start. It is the need to get ‘a feel’ for the task which I describe as the ‘Build-it’ stage; build a mental image or physically build a representation with manipulatives which enhance the understanding of the problem and helps children consider:

• what they do know
• what they need to know
• what they have enough information to ‘work out’?
• what information they need to work towards their solution
• what are the options if they don’t have the mathematical knowledge

To demonstrate this approach I gave the task below to a mixed group of secondary school mathematics and science teachers for whom GCSE Mathematics was the common qualification attained but for some it was ‘a quite a while ago’!

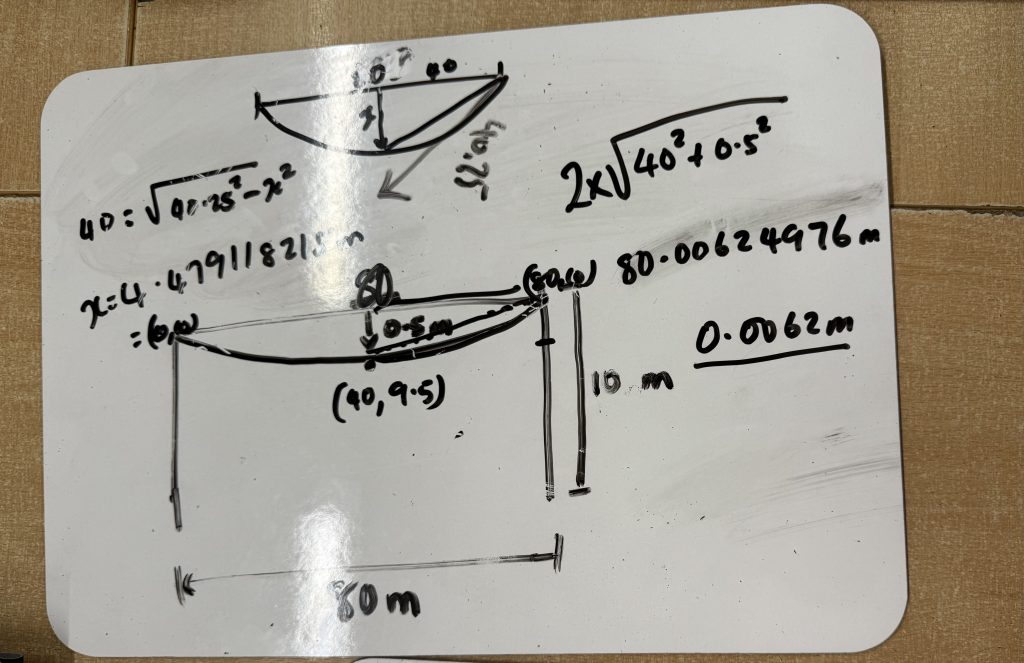
Teachers started by using their forearms to indicate the vertical telegraph poles and gesturing/ ‘air drawing’ whilst talking about a cable between the posts – “a straight line between the poles will be 80m and the cable should sag below the horizontal”

Already the shared language is key to supporting visualisation:

• straight
• vertical
• horizontal
• sag

Teachers talked of their mental picture of telegraph poles and to appreciating a distance of 80m related to a more commonly recognised distance of 100m track length. When it came to the gesturing the intended sag, the distance between the ends of fingers when pinching the first finger and thumb was an attempt to visualise the ‘smallness’ of 50cm length relative to their poles 80m apart.

Part 2 – using AI

It was at this point the teachers sketched on A3 White Boards (an ideal size for collaborative working) a representation of their visualisations and discussions so far; shared gestures, language and reasoning with explanations of:

• midpoint
• parabola
• symmetrical
• approximating lengths to line segments and calculate using Pythagoras Theorem

With the information available the mathematics gets more challenging (beyond GCSE) if you want to calculate the exact length of the cable forming an arc of a parabola, and this is where AI can assist. However, AI needs to be asked clear questions!

Let’s ask for the intended cable with a 50cm sag

1. What is the approximated length of the cable using the length of the line segments and Pythagoras Theorem – checking our calculation?
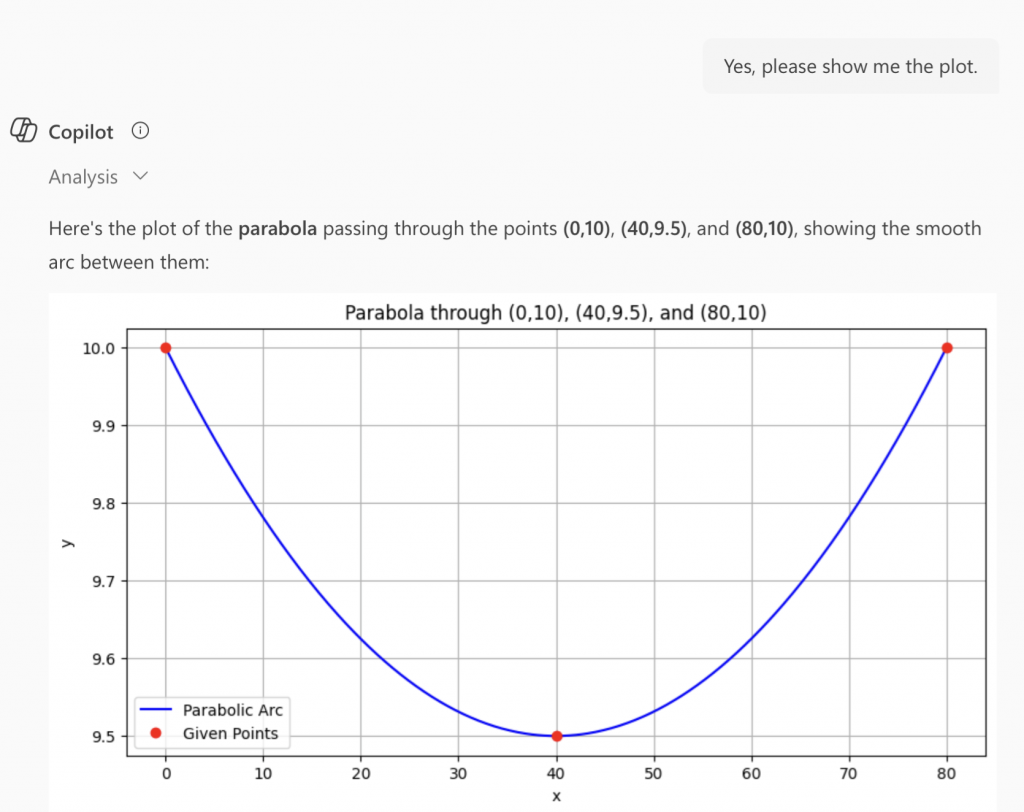
2. What is the calculated length of the parabola passing through the 3 identified points?
3. What does a graphical representation of the curve look like ( checking our sketches)?

The following includes our questions to Co-Pilot and the AI responses.

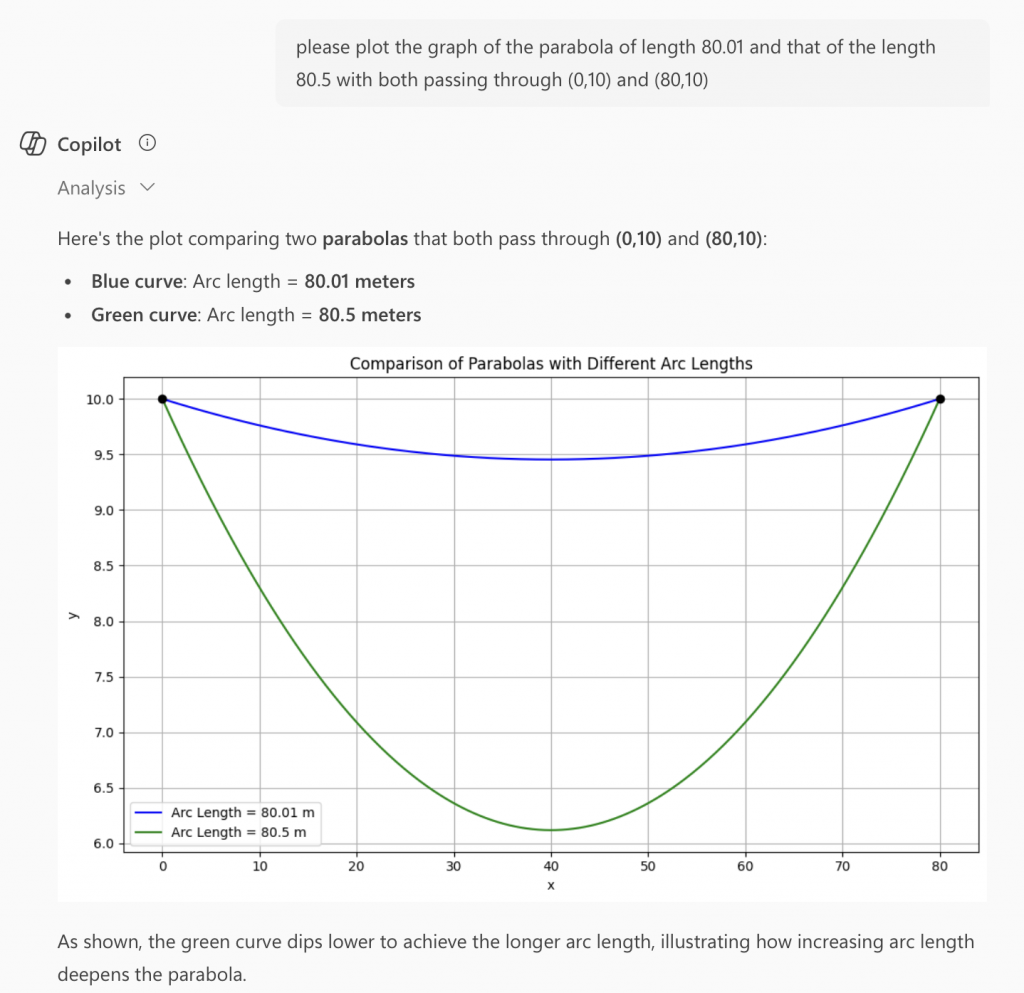
Now let’s ask about the ‘mistaken’ cable which has a length of 80.5m

1. What is the lowest point of the parabola passing through (0,10) and (80,10)?
2. What is the difference between the ‘intended’ sag of the cable and the ‘mistaken’ sag?

For AI to be useful, students (and teachers) need to

• follow a logical argument
• Identify and communicate the requirement of the task – can they describe what they want to build, in detail and guide the process?
• be curious, collaborative and resourceful
• ‘guesstimate’, reflect and check reasonableness/accuracy of AI responses

Supporting Metacognition

Visualisation, gestures, collaboration and articulating their ideas help children develop the skills needed for problem solving:

“comparing different students’ approaches to problem solving and decision making; identifying what is known, what needs to be known, and how to produce that knowledge; or having students think aloud while solving problems” (Costa, 1991)

 The school as a home for the mind: A collection of articles. Corwin. [Google Scholar]

• Modelling your thinking out loud helps pupils develop their own strategies

• Resilience is built by teaching children strategies for what to do when they do not know what to do.

• Identifying appropriate questions to ask in AI can support children as they work towards a solution