What does the data suggest
When reviewing the data of the national KS2 SATs 2024 outcomes by question, the eye is always drawn to the pieces of data that ‘buck the trend’. I am not aware that the data is expected to rigidly align with a statistical ‘line of best fit’ but is used here as a tool to assist when reviewing.
My attention was drawn to Question 13 on Paper 2, a mid-paper question and <50% of the cohort submitted a correct answer, approximately 11% less than might be anticipated using the ‘trend line’ of the graph below. Question 13 is on the topic of 3-D shape as is Question 23 on Paper 3, which received 23% of the cohort answering correctly, the lowest percentage and furthest below the trend line for any question on the paper.
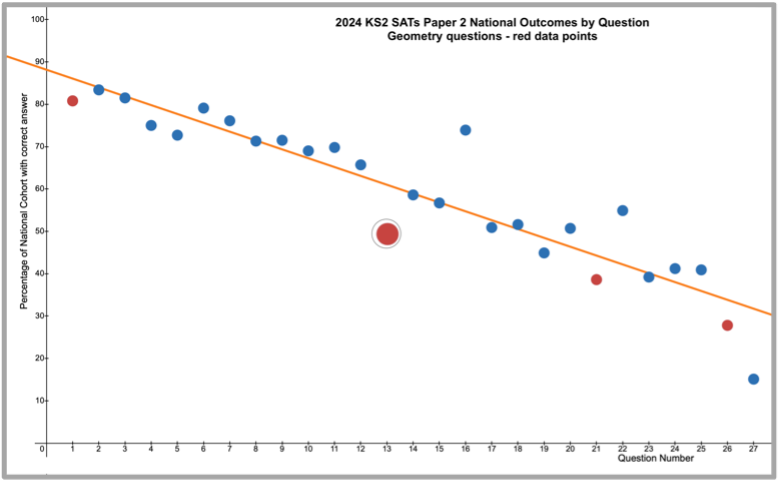
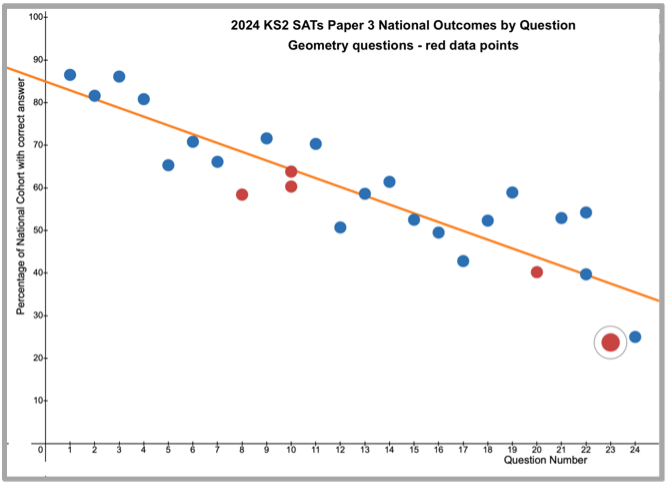
Whilst the circled red data points are questions focusing on 3-D shape only, it is worth noting all Geometry questions on Paper 2 (Qu’s 1,13, 21 and 26) and on Paper 3 (Qu’s 8, 10 ,20 and 23) fall below the ‘line of best fit’ in the graphs!
These are the 3-D Shape 2024 SATs questions:

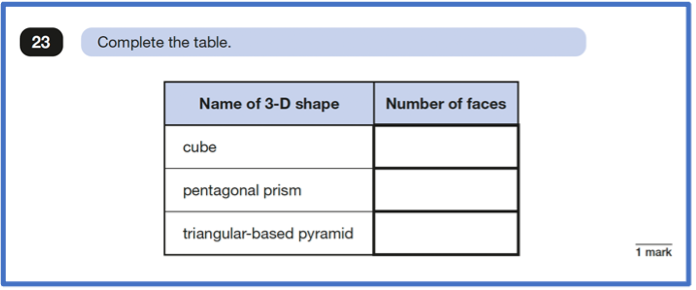
These two 3-D Shape questions primarily relate to National Curriculum content from Years 1-3 of the Programmes of Study for Mathematics (2013) with the KS2 expectation for children to recall mathematical subject knowledge and reason using the knowledge.
A key requirement for children to answer these questions would be to have a visual recall or mental image of the shapes. Based on the outcomes detailed above, it would suggest a significant proportion of children do not have a working command of this knowledge/skill. Insecure foundations are likely to impact on children when working at KS3/KS4.
The following offers support for teachers as to how this issue may be addressed:
Children need to be provided with the opportunity to develop a visual mental recall of 3-D Shapes
The need for children to ‘play’ and ‘explore’ when learning mathematics is not something to be restricted to EYFS and KS1. Play allows children to observe, make sense of and provide a concrete example to help communicate their thinking and understanding. Play is an essential part of children having the opportunity to develop the desirable mathematical behaviours of young mathematicians:
- to conjecture
- to predict
- to justify
- to compare and contrast
- to challenge another’s thinking through asking questions and discussion
- to generalise
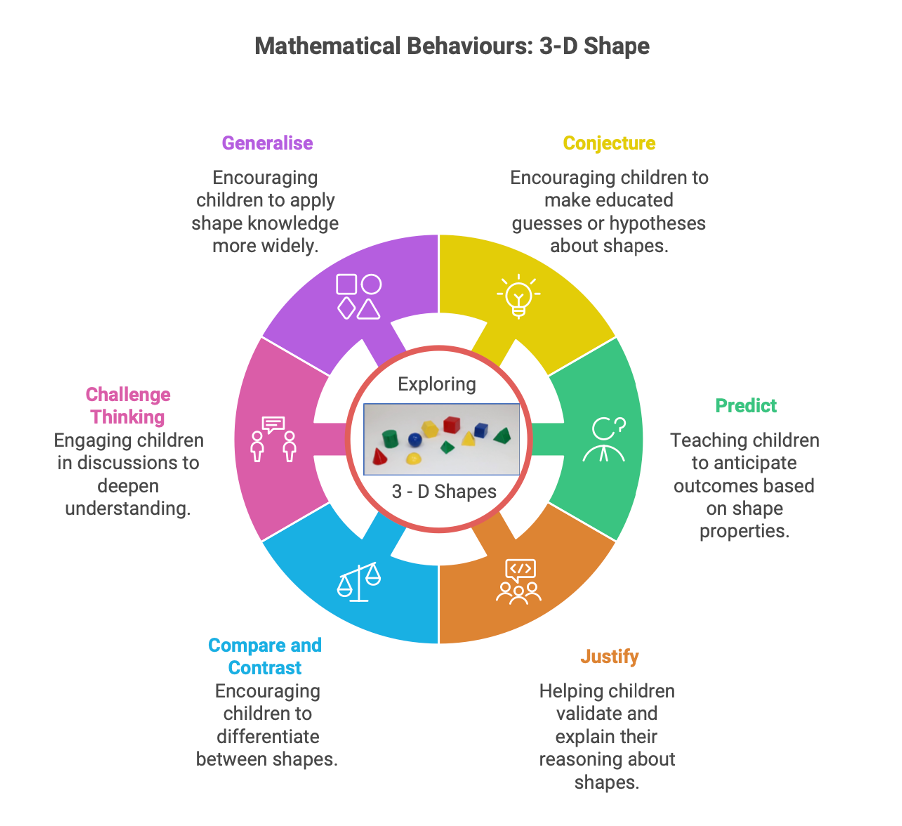
When children have a mental image/visual recall of 3-D shapes they are not reliant on separate memorised facts. The visualisation empowers the child to identify multiple facts, answer questions and reason solutions to problems.
“Talk in mathematics should not be seen simply as a rehearsal in class of the vocabulary of mathematics… It should extend to high-quality discussion that develops children’s logic, reasoning and deduction skills, and underpins all mathematical learning activity. The ultimate goal is to develop mathematical understanding – comprehension of mathematical ideas and applications.” The Williams Report (2008)
The Role of the teacher is to:
- provide learning opportunities/tasks for the children’s mathematical habits to be developed
- probe children’s thinking with appropriate questions
- introduce and refine mathematical language whilst allowing children to talk freely in a non-scripted manner
3-D Manipulatives
Provide the children with a suitable range of 3-D shapes to touch and hold, connect and separate, compare and sort.
E.g. A set of ten different 3-D shapes; cube, triangular prism, rectangular prism, hexagonal prism, triangular pyramid, square pyramid, sphere, hemisphere, cone and cylinder, each in 4 different colours provide opportunities for children to explore the content required for primary school learning. Note this set unlike many others includes a hexagonal prism encouraging children to think about 3-D shapes with polygons of more than 4 sides.

Tasks
The following tasks are intended for children to do in pairs or small groups. Each task can be adapted for the age and/or prior knowledge of the children when selecting the 3D shapes to be used. The purpose of the tasks is:-
- to encourage children to talk/discuss as they touch and play with the 3-D shapes
- to gather an insight into the key features of the shapes
- to support the development of visualising shapes – which is hard to achieve from looking at only diagrams
1. Feely bag
This task is for children to develop and use their sensory and oracy skills to describe 3-D shapes.
- A selection of 3-D shapes is placed in a non-transparent bag.
- One child puts their hand in the bag, selects one shape without removing the shape from the bag or looking inside.
- Using touch alone, the child must describe the selected shape to their partner/s, one detail at a time
- Partner/s suggest the identity of the shape either by naming it or pointing to what they think is the shape from a separate set of shapes
- Once children think they have identified the shape, it can be removed from the bag to check.
- Repeat the task with another child making the shape selection

Questions:
- What vocabulary/descriptions are most helpful?
- How many pieces of information do the children need to identify the shape correctly?
2. Sorting
This task is to help children to identify and categorise the key features of the 3-D shapes
- A selection of 3-D shapes is placed on a large piece of card.
- Working in pairs/small group children sort the physical shapes into 2 groups, agreeing the sort criteria.
- Allow children to describe the criteria using their own description which can be refined to mathematical language.
e.g. Shapes with a ‘Rounded surface’ (curved surface) and shapes without.

Questions:
- How do you decide which group a shape is to be placed (sorting criteria)?
- How can you sort the same selection of shapes in a different way?
- How are your sorted groups of shapes the same or different to another pair/groups? What criteria have they used to sort the shapes?
The task could be repeated using shapes with some common elements (Venn Diagram), or shapes sorted into 3 separate groups or 2 dimensional shapes could be included.
3. What’s my shape?
This task is to encourage children to ask questions and in doing so develop, refine and practice their skills in precision of questioning and use of mathematical language.
- Two children face each other with a white board or similar acting as a barrier between them and ensuring neither can see what is on the opposite side. Alternatively, children could sit back to back.
- A child selects a 3-D shape and hides it from their partner behind the barrier.
- The partner must ask questions to identify the hidden shape.
- Initially allow questions to be open, however as the task is repeated it can be more challenging if the child with the shape can only respond with Yes or No to questions.

Questions:
- What questions could the partner ask the child to help them identify the shape? E.g.
- Are all the faces the same shape?
- How many faces does the shape have?
- Does it have a ‘pointy’ end?
- What refinements can be made to a question/answer? (supported by the teacher) e.g.
- “What is the mathematical term for a ‘corner’?”
- Is the end at the top or the bottom – does it matter, is the orientation important?
- Are some questions more helpful/informative than others? – make a list of ‘good’ questions
4. WODB – Which one doesn’t belong
This task is for children to practice and strengthen their visualising skills, critical and creative thinking with reasoning.
- The names of different 3-D shapes/objects are placed on the 4 sections of the card.
- Children will need to visualise the four shapes/objects and use their knowledge of the shapes to reason which they consider to be the ‘odd one out’ based on the attributes of the shapes.
- The choice of shapes/objects should not lead to there being only one correct answer.
- Encourage children to think creatively when looking for attributes
- A collection of cards can be made for future use and could include landmarks etc which link with a recent humanities topic.
E.g. WODB – with possible reasons for selection
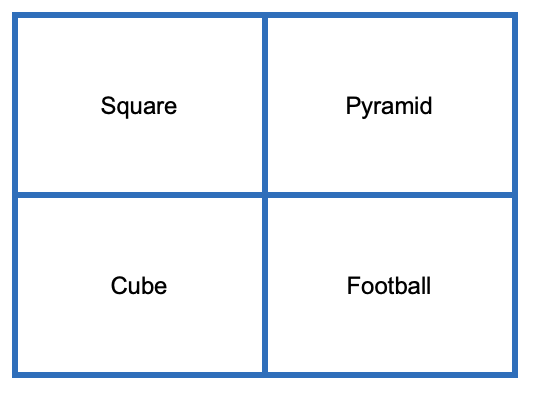
Football because
- it is made up of hexagons and pentagons
- it has a curved surface
Square because
- it is 2-D
- it has 4 sides (not edges)
Cube because
- all faces are equal in area
- a regular polyhedron (3-D shape)
Pyramid because
- it has triangular faces
- it has a point (apex) when its base is on the table
Questions
- Do all pyramids have the same shape base?
- Are all footballs made from Hexagons and Pentagons?
- What’s the difference between a pyramid and a prism?
- Which 3-D shapes always have the same shape face at either end?
- What other shapes have an apex?
National Curriculum Statements DFE Reference 00180-2013

Use of question copyright from https://www.nationalarchives.gov.uk/doc/open-government-licence/version/3/
About the author
Pip Huyton is a mathematics consultant working in both the primary and secondary sectors. Her roles involve being a trainer, adviser, facilitator, often in a bespoke school improvement capacity. Interests include curriculum development, the use of manipulatives for supporting children developing conceptual understanding and effective use of dynamic technology for learning.
Authored:
- Build-it Say-it Write-it Understanding the concepts of Perimeter and Area using Manipulatives
ISBN 978-1-912185-32-0 available via Association of Teachers of Mathematics
- KS1 Assessment Tasks Not Tests
Freely available via Association of Teachers of Mathematics and Mathematical Association websites
Contact
- Email: pip@accomplisheducation.com
Leave a Reply